LEYES DE NEWTON

 

INTRODUCCIÓN:         

 

Isaac Newton sentó las bases de la mecánica, definiendo conceptos fundamentales de masa,
tiempo, fuerza entre otros de modo más preciso y estableció las 3 leyes que explican el movimiento de cualquier objeto del universo, se trata de Las Leyes de Newton que son los 3 principios a partir de los cuales se explica una gran parte de los problemas planteados en mecánica clásica.

PRIMERA LEY DE NEWTON

 

También se denomina Ley de la INERCIA. Sabemos por la experiencia que, para que un balón en reposo se ponga en movimiento, debemos aplicar una fuerza sobre ella. Del mismo modo, si este balón se mueve con velocidad constante, es preciso aplicarle una fuerza para que se detenga.

 

 

 

LA INERCIA ES LA TENDENCIA NATURAL DE LOS OBJETOS A PERMANECER EN REPOSO O EN MOVIMIENTO RECTILÍNEO UNIFORME.

https://es.wikipedia.org/wiki/Inercia

 

CLASIFICACIÓN:

 

La INERCIA MECÁNICA se divide en 5 tipos:

 

• INERCIA DINÁMICA: Se relaciona con los cuerpos que se encuentran es estado de movimiento.
• INERCIA ESTÁTICA: Esta es aquella que está vinculada con los cuerpos en estado de reposo.
• INERCIA TRASLACIONAL: Es la vinculada con la masa total de un cuerpo.
• INERCIA ROTACIONAL: Se trata de aquella que representa la propiedad de los cuerpos para resistir los cambios de su estado de movimiento rotatorio, se le identifica con el símbolo.
• INERCIA TÉRMICA: Se le llama así a la propiedad que nos indica la cantidad de calor que pueden conservar los cuerpos, así como la con que estos pueden absorber el calor o cederlo.

 

 

EJEMPLOS RESUELTOS

 

Ejemplos de acciones de la vida cotidiana en que se aplique la LEY DE LA INERCIA

 

1. El que al quitar un mantel rápidamente de una mesa, quedando puesto lo que se tenga arriba del mantel, es producto de la inercia.

2. Cuando corremos a alta velocidad nos cuesta más trabajo detenernos gracias a la inercia.

 

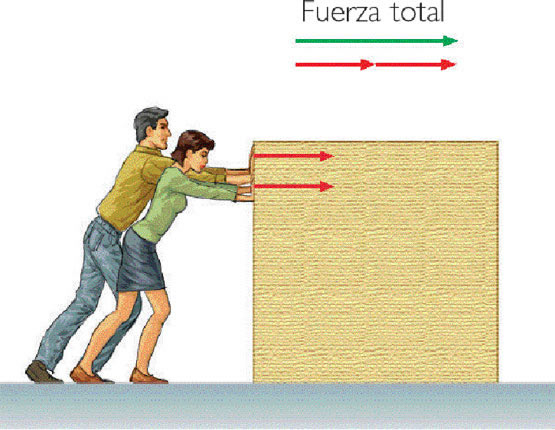
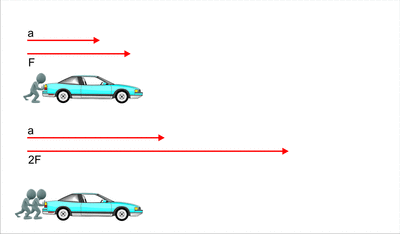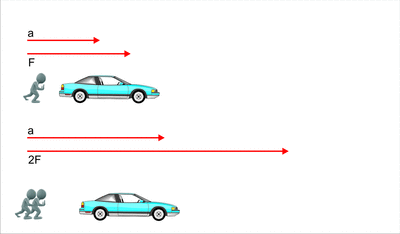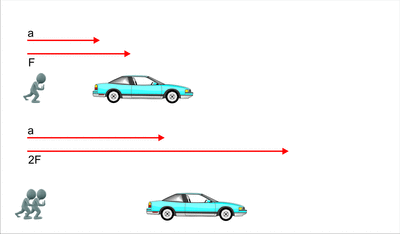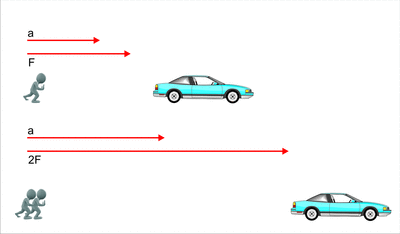
3. Cuando se empuja un auto que está en reposo, al principio cuesta trabajo debido a la inercia que se opone al movimiento, una vez que se empieza a mover es más fácil empujarlo, gracias a la inercia que tiene ahora en movimiento.

4. Cuando un automóvil da una vuelta los pasajeros sienten una fuerza que los empuja a seguir la dirección del movimiento inicial, esto se debe a que la inercia que llevaban era en esa dirección.

 

5. Dar la vuelta en un barco cuesta más trabajo que en una lancha, ya que la inercia del barco es mucho mayor que la de la lancha.


EJEMPLOS A RESOLVER

Como influye la Ley de INERCIA en las siguientes actividades de la vida cotidiana

a) En el ascensor

b) En el autobús

SOLUCIÓN

 a) EN EL ASCENSOR: En el momento que este comienza a moverse hacia arriba sentimos una fuerza ascensional sobre los pies, pues nuestra tendencia o inercia es a permanecer en reposo, estado que es alterado.

b) EN EL AUTOBÚS: Cuando arranca, nos sentimos desplazados hacia atrás, y cuando frena, nos movemos hacia adelante. En ambos casos se pone en manifiesto una tendencia a permanecer en estado de reposo o de movimiento rectilíneo uniforme.

CONCLUSIÓN

 TODO CUERPO PERMANECE EN ESTADO

 DE REPOSO O DE MOVIMIENTO RECTILINEO

 UNIFORME A NO SER QUE ACTÚE SOBRE EL

 ALGUNA FUERZA NETA O RESULTANTE

 

 

 

 

 



 

SEGUNDA LEY DE NEWTON

“El cambio de movimiento es directamente proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime”

Esta ley se encarga de cuantificar el concepto de fuerza. La aceleración que adquiere un cuerpo es proporcional a la fuerza neta aplicada sobre el mismo. La constante de proporcionalidad es la masa del cuerpo (que puede ser o no ser constante). Entender la fuerza como la causa del cambio de movimiento y la proporcionalidad entre la fuerza impresa y el cambio de la velocidad de un cuerpo es la esencia de esta segunda ley.^[]

 CARACTERÍSTICAS:

 

 

1.- La aceleración que adquiere un cuerpo es proporcional a la fuerza aplicada, y la constante de proporcionalidad es la masa del cuerpo.

2.- Si actúan varias fuerzas, esta ecuación se refiere a la fuerza resultante, suma vectorial de todas ellas.

3.- Esta es una ecuación vectorial, luego se debe cumplir componente a componente.

FÓRMULA:             
                                                  F= m a

 

 

EJERCICIOS RESUELTOS:

Un bloque por la acción de una fuerza resultante de 2kgf adquiere una aceleración de 400 cm/s2 para calcular en kg la masa del bloque.

 F= m*a                                                        2kgf*9,8 = 19,6N     400 cm/s2 = 4 m/s2
m= F/ a
m= 19,6 N / 4 m/s2
m= 4,9 kg


En una publicidad de un auto de 1000 kg se afirma que es capaz de alcanzar una velocidad de 108 km/h en 10s partiendo del reposo. ¿Qué fuerza deberá ejercer el motor?

a= Vf - Vo / t                                                    F= m*a

a= 30m/s2 - o / 10s2                                         F= 1000kg * 3m/s2

a= 3m / s2                                                        F= 333,33 N

 EJERCICIOS A RESOLVER

- Un cuerpo de masa igual a 2kg se desplaza con una aceleración de 6m/s2. ¿ Cuál es el valor de la fuerza según la segunda ley de Newton?

- Un disco de hockey de masa, se desliza sobre una superficie horizontal sin fricción de una pista de hielo, 2 bastones golpean a la pelota con fuerzas de 5 y 8 N respectivamente. ¿ Cuál es la aceleración que ejerce cada bastón?

- Una fuerza de proporción a la masa 2,5kg y una aceleración de 1,2 m/s2. Calcular la magnitud de la fuerza en Newton https://es.wikipedia.org/wiki/Leyes_de_Newton


CONCLUSIÓN

Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.

 

TERCERA LEY DE NEWTON

 

La tercera ley de Newton establece lo siguiente:

 

                    Siempre que un objeto ejerce una fuerza sobre un segundo objeto, el segundo objeto ejerce una fuerza de igual magnitud y dirección opuesta sobre el primero.  Con frecuencia se enuncia como "A cada acción siempre se opone una reacción igual".  En cualquier interacción hay un par de fuerzas de acción y reacción, cuya magnitud es igual y sus direcciones son opuestas. Las fuerzas se dan en pares, lo que significa que el par de fuerzas de acción y reacción forman una interacción entre dos objetos.

 

 

CARACTERÍSTICAS:

 

1. Más que referirse a la relación entre fuerza y movimiento, ayuda a comprender las características comunes que tienen todas las fuerzas que actúan sobre los cuerpos. Toda fuerza resulta de la interacción de, por lo menos, dos objetos.
2. Newton observó que durante este proceso, los dos cuerpos se ven afectados y se deforman, o alteran su estado de movimiento. Si lanzas un huevo contra otro, los dos se rompen; si aplaudes violentamente, las dos manos te duelen; cuando dos canicas chocan, ambas se desvían.

 

 

 EJEMPLOS EN LA VIDA CONTIDIANA SOBRE ACCIÓN Y REACCIÓN

 

Al patear una pelota, el pie ejerce una fuerza sobre ésta; pero, al mismo tiempo, puede sentirse una fuerza en dirección contraria ejercida por la pelota sobre el pie.

Si una persona empuja a una pared la pared. La persona ejerce una fuerza sobre la pared y la pared otra fuerza sobre la persona.

Cuando una persona camina empuja hacia atrás el suelo, la reacción del suelo es empujarlo hacia adelante, por lo que se origina un movimiento de la persona hacia adelante. Lo mismo sucede con un auto en movimiento, las ruedas empujan el camino y este la empuja hacia adelante.

Un objeto colgando de una cuerda ejerce una fuerza sobre la cuerda hacia abajo, pero la cuerda ejerce una fuerza sobre este objeto hacia arriba, dando como resultado que el objeto siga colgando y no caiga.

EJERCICIOS RESUELTOS:http://locosporlafisic.blogspot.com/2013/04/ejercicios-de-la-tercera-ley-de-newton.html#!/2013/04/ejercicios-de-la-tercera-ley-de-newton.html
1. Consideramos un cuerpo con un masa m = 2 Kg. que está en reposo sobre un plano horizontal, como el indicado en la figura 17. a) Haz un diagrama de cuerpo libre. b) Calcular la fuerza con que el plano reacciona contra el bloque.

 

 a) Las fuerzas que actúan sobre el bloque están representadas en la figura 18, donde se elije un eje de coordenadas cuyo origen es el centro del cuerpo, mostrándose las fuerzas verticales: el peso  y la normal 

b) Para calcular la fuerza que el plano ejerce sobre el bloque aplicamos la segunda ley de Newton:

Como  actúa hacia arriba y   actúa hacia abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:

N – P = m . a

Como en la dirección vertical no hay movimiento entonces la aceleración es cero (a = 0), luego

N – P = 0

N = P

N = m . g (porque P = m ( g)

Sustituyendo los valores de m y g se tiene:

N = 2 Kg . 9,8 m/s2

N = 19,6 N

Esta es la fuerza con que el plano reacciona sobre el bloque.

 2. En la figura 19 se muestran dos masas M1 = 3 Kg. y M2 = 5 Kg. colgando de los extremos de un hilo que pasa por la garganta de una polea a) Hacer un diagrama de las fuerzas que actúan b) Calcular la tensión del hilo y la aceleración con que se mueve el sistema.

 a) Obsérvese la figura 20(a), la cual representa el diagrama del cuerpo libre para el cuerpo de masa M1.

 Es la tensión del hilo, actuando hacia arriba.

    El peso del cuerpo de masa M1.

En la figura 20(b) se muestra el diagrama de cuerpo libre para el cuerpo de masa M2.

 Es la tensión del hilo, actuando hacia arriba.

 El peso del cuerpo de masa M2.

b) Como el cuerpo de masa M1 sube, la tensión T es mayor que P, por lo que podemos escribir en módulo la segunda ley de Newton así:

T – P1 = M1 . a.………………………………………… (A)

Como el cuerpo de masa M2 baja, el peso P2 es mayor que T, pudiéndose escribir en módulo la segunda ley de Newton así:

P2 – T = M2 . a.………………………………………… (B)

Despajando T de la ecuación (A) nos queda que:

T = M1 . a + P1

Sustituyendo ésta expresión en (B) tenemos:

P2 – (M1 . a + P1) = M2 . a

P2 – P1 = M2 . a + M1 . a

Sacando a como factor común:

P2 – P1 = a . (M2 + M1)

Despejando nos queda:

(C)

Calculemos por separado P1 y P2

P1 = M1 . g = 3 Kg . 9,8 m/s2

P1 = 29,4 N

P2 = M2 . g = 5 Kg. . 9,8 m/s2

P2 = 49 N

Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:

 La tensión la obtenemos sustituyendo en la expresión:

T = M1 .  a + P1

T = 3 Kg .  2,45 m/s2 + 29,4 N

T = 7,35 N + 29,4 N

T = 36,4 N

Luego y T = 36,4 N

EJERCICIOS A RESOLVERhttps://www.fisicalab.com/apartado/principio-accion-reaccion#contenidos

 3. En la figura 21 se muestran dos bloques de masa M2 = 2 Kg. que arrastra sobre el plano horizontal al cuerpo de masa M1 = 7 Kg. Calcular la aceleración del sistema y tensión de la cuerda.
4.Dos niños, Juan de 20kg y Pedro de 25kg, están frente a frente en una pista de hielo. Juan da un empujón a Pedro y este sale despedido con una rapidez de 3m/seg. Calcular la rapidez con que retrocede Juan, suponiendo que los patines no ofrecen resistencia al movimiento
 5.Dos niños están patinando sobre una pista de hielo. Se empujan y salen despedidos con velocidades de 3m/seg y 3,5m/seg. Si la masa del primer niño es de 25kg, calcular la masa del segundo.

 http://leyes-de-newton-fisica.blogspot.com/p/ejercicios.html

 

VIDEO PERSONAL , SOBRE EXPERIMENTOS DE LAS 3 LEYES DE NEWTON