SEGUNDA LEY DE NEWTON

“El cambio de movimiento es directamente proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime”

Esta ley se encarga de cuantificar el concepto de fuerza. La aceleración que adquiere un cuerpo es proporcional a la fuerza neta aplicada sobre el mismo. La constante de proporcionalidad es la masa del cuerpo (que puede ser o no ser constante). Entender la fuerza como la causa del cambio de movimiento y la proporcionalidad entre la fuerza impresa y el cambio de la velocidad de un cuerpo es la esencia de esta segunda ley.^[]

 CARACTERÍSTICAS:

 

 

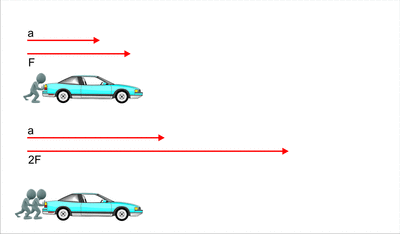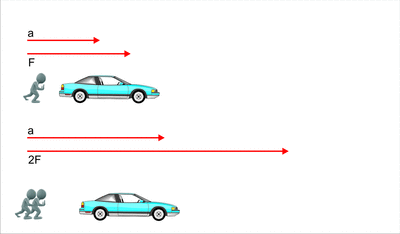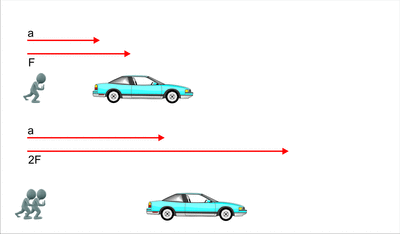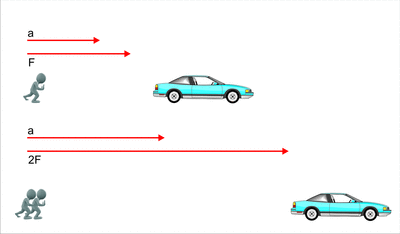
1.- La aceleración que adquiere un cuerpo es proporcional a la fuerza aplicada, y la constante de proporcionalidad es la masa del cuerpo.

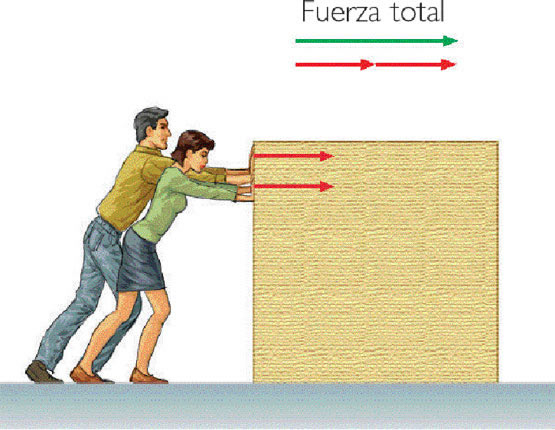
2.- Si actúan varias fuerzas, esta ecuación se refiere a la fuerza resultante, suma vectorial de todas ellas.

3.- Esta es una ecuación vectorial, luego se debe cumplir componente a componente.

FÓRMULA:             
                                                  F= m a

 

 

EJERCICIOS RESUELTOS:

Un bloque por la acción de una fuerza resultante de 2kgf adquiere una aceleración de 400 cm/s2 para calcular en kg la masa del bloque.

 F= m*a                                                        2kgf*9,8 = 19,6N     400 cm/s2 = 4 m/s2
m= F/ a
m= 19,6 N / 4 m/s2
m= 4,9 kg


En una publicidad de un auto de 1000 kg se afirma que es capaz de alcanzar una velocidad de 108 km/h en 10s partiendo del reposo. ¿Qué fuerza deberá ejercer el motor?

a= Vf - Vo / t                                                    F= m*a

a= 30m/s2 - o / 10s2                                         F= 1000kg * 3m/s2

a= 3m / s2                                                        F= 333,33 N

 EJERCICIOS A RESOLVER

- Un cuerpo de masa igual a 2kg se desplaza con una aceleración de 6m/s2. ¿ Cuál es el valor de la fuerza según la segunda ley de Newton?

- Un disco de hockey de masa, se desliza sobre una superficie horizontal sin fricción de una pista de hielo, 2 bastones golpean a la pelota con fuerzas de 5 y 8 N respectivamente. ¿ Cuál es la aceleración que ejerce cada bastón?

- Una fuerza de proporción a la masa 2,5kg y una aceleración de 1,2 m/s2. Calcular la magnitud de la fuerza en Newton https://es.wikipedia.org/wiki/Leyes_de_Newton


CONCLUSIÓN

Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.